An inscribed angle is half the measure of a central angle subtended by the same arc.

OR

A central angle is twice the measure of an inscribed angle subtended by the same arc.

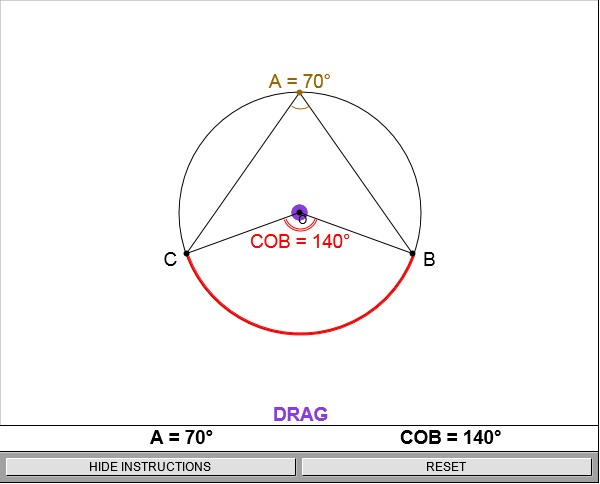
In each of the figures below, CAB is half the size of COB since both are subtended by arc(CB).

Alternately, COB is twice the size of CAB since both are subtended by arc(CB).

Note that a consequence of this property is that any inscribed angle subtended by a semicircle is a right angle, as shown in the example above right.

Click here for an mathematical explanation of WHY the Central Angle Property works.

Note that this is not a PROOF but an EXPLANATION.